树状数组

发表于 | 更新于 | 阅读次数：

树状数组是一种非常好打优美的数据结构，适用性十分广泛，而且常数非常小。

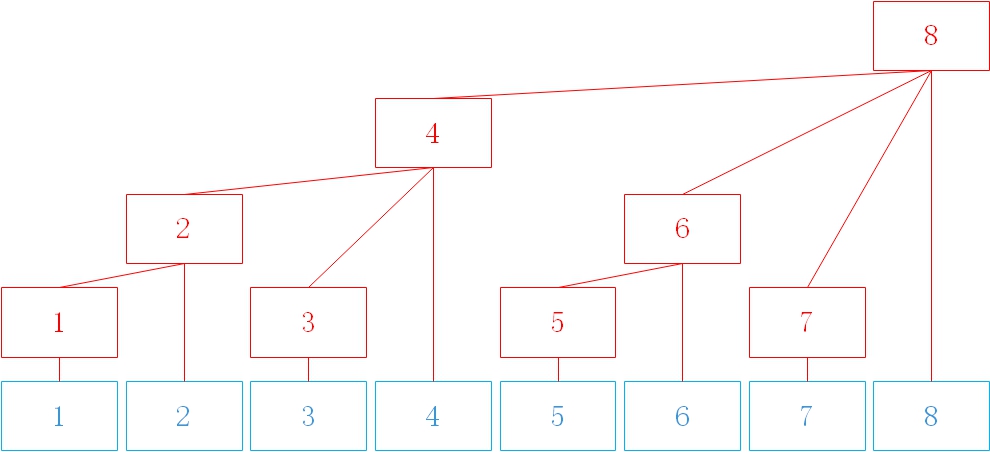
（自己花五分钟做的图）

下面蓝色的是我们的原数组，红色的即是我们的 $tree$ 数组。

树状数组的主旨是单点修改，查询前缀和，它的核心是 $\rm lowbit$

如 $\rm lowbit((111)_2) = (001)_2,\rm lowbit((110)_2) = (010)_2$

即 $\rm lowbit(7) = 1,\rm lowbit(6) = 2$

仔细观察原树，不难发现：

$$tree[i]=\sum\limits_{j=i-lowbit(i)+1}^i a[j]$$

于是我们所求的前缀和可以由 $tree$ 数组得出

$$sum[i] = tree[i] + tree[i - lowbit(i)] + tree[(i - lowbit(i)) - lowbit(i - lowbit(i))] ...$$

举个栗子：

$$sum[(111)_2] = tree[(111)_2] + tree[(110)_2] + tree[(100)_2]$$

这里需要仔细看几遍才能理解。

于是查询前缀和的操作就写好了。

1
2
3
4
5
6
7
ll query(int p) // 查询前缀和
{
	ll res = 0;
	while (p)
		res += tree[p], p -= (p & -p);
	return res; 
}

接下来考虑单点修改

当 $a[i]$ 改变的时候，所有包含 $i$ 这个位置的 $tree[j]$ 均要改变。

树状数组是一棵树！

于是我们只需要找到 $tree[i]$ 的父亲，以及它的父亲的父亲爷爷...逐个更新

而再次仔细观察，我们惊奇的发现：

节点 $i$ 的父亲编号即为 $i + \rm lowbit(i)$ !

1
2
3
4
5
void add(int p, ll x) // 单点修改
{
	while (p <= n)
		tree[p] += x, p += (p & - p);
}

单点修改 + 区间查询

知道前缀和很容易计算出区间和。

区间 $[l,r]$ 的和即为 $sum[r] - sum[l-1]$ 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void add(int p, ll x)
{
	while (p <= n)
		tree[p] += x, p += (p & - p);
}

ll query(int p)
{
	ll res = 0;
	while (p)
		res += tree[p], p -= (p & -p);
	return res; 
}

ll range_query(int l, int r)
{
	return query(r) - query(l - 1);
}

区间修改 + 单点查询

这里我们要用到神奇的差分。

新建 $d$ 数组。

$$d[1]=a[1],d[i]=a[i]-a[i-1] (2\le i \le n)$$

可以得出:

$$a[p]=\sum\limits_{i=1}^{p}d[i]$$

这是啥？不就是前缀和嘛！

而当区间 $[l,r]$ 全部加上 $x$ 时，我们只需将 $d[l]$ 加上 $x$ ，$d[r + 1]$ 减去 $x$ 就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void add(int p, ll x)
{
	while (p <= n)
		tree[p] += x, p += (p & - p);
}

void range_add(int l, int r, ll x)
{
	add(l, x), add(r + 1, -x);
}

ll query(int p)
{
	ll res = 0;
	while (p)
		res += tree[p], p -= (p & -p);
	return res; 
}

区间修改 + 区间查询

这是最常用的算法，第一次看到的时候真的惊艳到我了。

$$sum[p]=\sum\limits_{i=1}^p a[i] = \sum\limits_{i=1}^p \sum\limits_{j=1}^i d[j]$$

仔细看，发现 $d[1]$ 加了 $p$ 次， $d[2]$ 加了 $p-1$ 次， $d[3]$ 加了 $p-2$ 次...

于是可以继续推：

$$sum[p]=\sum\limits_{i=1}^p d[i] \times (p - i + 1)$$

$$=(p+1)\times\sum\limits_{i=1}^p d[i] - \sum\limits_{i=1}^p d[i] \times i$$

于是我们只需要同时维护 $\sum\limits_{i=1}^p d[i]$ 与 $\sum\limits_{i=1}^p d[i] \times i$ 便可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void add(int p, ll x)
{
	for (int i = p; i <= n; i += (i & -i))
		tree1[i] += x, tree2[i] += x * p;
}

void range_add(int l, int r, ll x)
{
	add(l, x), add(r + 1, -x);
}

ll query(int p)
{
	ll res = 0;
	for (int i = p; i; i -= (i & -i))
		res += (p + 1) * tree1[i] - tree2[i];
	return res; 
}

ll range_query(int l, int r)
{
	return query(r) - query(l - 1);
}