列举一些我常用的网站。

顺便方便下我自己

题目描述

C 国有 $n$ 个大城市和 $m$ 条道路，每条道路连接这 $n$ 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 $m$ 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 $1$ 条。

C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 $n$ 个城市的标号从 $1\sim n$ ，阿龙决定从 $1$ 号城市出发，并最终在 $n$ 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 $n$ 个城市。

阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 C 国有 $5$ 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

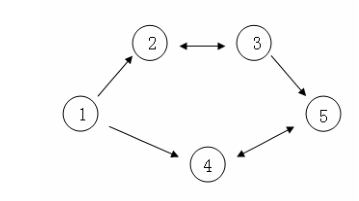
假设 $1\sim n$ 号城市的水晶球价格分别为 $4,3,5,6,1$ 。

阿龙可以选择如下一条线路：$1\rightarrow 2 \rightarrow 3 \rightarrow 5$，并在 $2$ 号城市以 $3$ 的价格买入水晶球，在 $3$ 号城市以 $5$ 的价格卖出水晶球，赚取的旅费数为 $2$ 。

阿龙也可以选择如下一条线路 $1\rightarrow 4 \rightarrow 5 \rightarrow 4 \rightarrow 5$，并在第 $1$ 次到达 $5$ 号城市时以 $1$ 的价格买入水晶球，在第 $2$ 次到达 $4$ 号城市时以 $6$ 的价格卖出水晶球，赚取的旅费数为 $5$ 。

现在给出 $n$ 个城市的水晶球价格， $m$ 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

$n$ 个人围成一圈,编号按顺序从 $0$ 到 $n-1$，从第一个人开始报数,数到 $m$ 的人出列,再由下一个人重新从 $1$ 开始报数,数到 $m$ 的人再出圈,……依次类推,直到所有的人都出圈,请输出最后一个出圈的人的编号。

题目描述

小城和小华都是热爱数学的好学生，最近，他们不约而同地迷上了数独游戏，好胜的他们想用数独来一比高低。但普通的数独对他们来说都过于简单了，于是他们向 $Z$ 博士请教，$Z$ 博士拿出了他最近发明的“靶形数独”，作为这两个孩子比试的题目。

靶形数独的方格同普通数独一样，在 $9$ 格宽 $\times 9$ 格高的大九宫格中有 $9$ 个 $3$ 格宽 $\times 3$ 格高的小九宫格 $($ 用粗黑色线隔开的 $)$。在这个大九宫格中，有一些数字是已知的，根据这些数字，利用逻辑推理，在其他的空格上填入 $1$ 到 $9$ 的数字。每个数字在每个小九宫格内不能重复出现，每个数字在每行、每列也不能重复出现。但靶形数独有一点和普通数独不同，即每一个方格都有一个分值，而且如同一个靶子一样，离中心越近则分值越高。$($ 如图 $)$

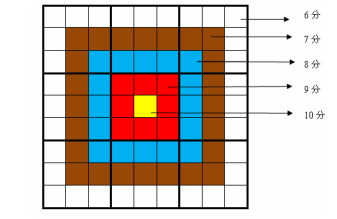
上图具体的分值分布是：最里面一格 $($ 黄色区域 $)$ 为 $10$ 分，黄色区域外面的一圈 $($ 红色区域 $)$ 每个格子为 $9 $分，再外面一圈 $($ 蓝色区域 $)$ 每个格子为 $8$ 分，蓝色区域外面一圈 $($ 棕色区域 $)$ 每个格子为 $7$ 分，最外面一圈 $($ 白色区域 $)$ 每个格子为 $6$ 分，如上图所示。比赛的要求是：每个人必须完成一个给定的数独 $($ 每个给定数独可能有不同的填法 $)$，而且要争取更高的总分数。而这个总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和

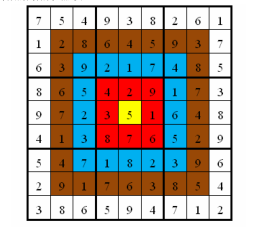
总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和。如图，在以下的这个已经填完数字的靶形数独游戏中，总分数为 $2829$ 。游戏规定，将以总分数的高低决出胜负。

题目描述

给出一个 $n \times n$ 的矩阵，矩阵中，有些格子被染成白色，有些格子被染成黑色，现要求矩阵中白色矩形的数量。

题目描述

有 $n$ 对情侣来到电影院观看电影。在电影院，恰好留有 $n$ 排座位，每排包含 $2$ 个座位，共 $2\times n$ 个座位。

现在，每个人将会随机坐在某一个位置上，且恰好将这 $2\times n$ 个座位坐满。

如果一对情侣坐在了同一排的座位上，那么我们称这对情侣是和睦的。

你的任务是求出共有多少种不同的就坐方案满足恰好有 $k$ 对情侣是和睦的。

两种就坐方案不同当且仅当存在一个人在两种方案中坐在了不同的位置。不难发现，在没有任何限制条件的情况下，每个人任意就坐一共会有 $(2n)!$ 种不同的就坐方案。

这里会简单记录我学习的基础数论。这里的证明可能都不大严谨，仅供参考。

欧几里得算法

如果我们想要求 $gcd(a,b)$ ，最简单的方式便是枚举，但这太慢了。

于是我们有了我们的辗转相除法，也就是欧几里得算法，它可以在 $O(log(a+b))$ 的复杂度内求出 $gcd(a,b)$ 。

$$\forall a,b \in \mathbb{N}, b \not = 0,\quad gcd(a,b) = gcd(b,a\bmod b)$$

证明

$a < b$ 时

$gcd(b,a \bmod b)=gcd(b,a)=gcd(a,b)$

$a \geq b$ 时

设 $r=a\bmod b$ ，$d$ 为 $a,\,b$ 任意一个公约数。

则 $a=kb+r,\;a\equiv b\equiv 0 \pmod{d}$

$\therefore a-kb\equiv r \equiv 0 \pmod{d}$

$\therefore d\,|\,b,\,d\,|\,a\bmod b$

所以 $a,b$ 和 $b, a \bmod b$ 的公约数集合是相同的，它们的最大公约数必然也相等。

$\therefore gcd(a,b)=gcd(b, a \bmod b)$

要注意边界：$b = 0$ 时，$gcd(a,b) = a$

代码

1
2
3
4

int gcd(int a, int b)
{
	return !b ? a : gcd(b, a % b);
}

好久没有更新了，来写 $(shui)$ 一篇 $LCA$ 的博客。

以前觉得 $LCA$ $($最近公共祖先$)$是神仙学的东西， $fj$ 讲的时候我也贼吉尔懵逼，现在看来也没有那么难。

当我们想求 $LCA(x,y)$ 时，如果一格一格跳直到跳到同一位置，不知道会跳到哪一年去，于是我们用到了一个神奇的东西：倍增。

众所周知任何数都可以用二进制，所以我们可以每次跳 $2^i$ 步，大大加快效率。这里我们用 $fa[i][j]$ 代表第 $i$ 号节点往上跳 $2^j$ 步到达的位置。所以很容易推出来: $fa[i][j]=fa[fa[i][j-1]][j-1]$ 。

然后跳的具体过程看代码。

题目背景

盛夏，冰之妖精琪露诺发现了一大片西瓜地，终于可以吃到美味的冻西瓜啦。

题目描述

琪露诺是拥有操纵冷气程度的能力的妖精，一天她发现了一片西瓜地。这里有 $n$ 个西瓜，由 $n-1$ 条西瓜蔓连接，形成一个有根树，琪露诺想要把它们冷冻起来慢慢吃。

这些西瓜蔓具有神奇的性质，可以将经过它的冷气的寒冷程度放大或缩小，每条西瓜蔓放大/缩小冷气寒冷程度的能力值为 $W_i$ ，表示冷气经过它后，寒冷程度值 $x$ 会变为 $x\times w_i$ 。每个西瓜也有一个寒冷程度值，炎热的夏日，所有西瓜的寒冷程度值初始都为 $0$ 。

琪露诺会做出两种动作:

①.对着西瓜 $i$ 放出寒冷程度为 $x$ 的冷气。这股冷气顺着西瓜蔓向“西瓜树”的叶子节点蔓延，冷气的寒冷程度会按照上面的规则变化。遇到一个西瓜连了多条西瓜蔓时，每条叶子节点方向的西瓜蔓均会获得与原先寒冷程度相等的冷气。途径的所有西瓜的寒冷程度值都会加上冷气的寒冷程度值。

⑨.向你询问西瓜 $i$ 的寒冷程度值是多少。

等等，为什么会有⑨？因为笨蛋琪露诺自己也会忘记放了多少冰呢。

所以，帮她计算的任务就这么交给你啦。